Premenné

Contents

Premenné #

Všetky premenné v jazyku dpic sú numerické a sú nad nimi definované aritmetické a logické operácie. Súradnice bodu na ploche majú definovanú polohu usporiadanou dvojicou numerických hodnôt $(x,y)$, ktoré sú dostupné ako preddefinované atribúty .x,.y. Súradnice bodu nie je možné použiť ako hodnotu premennej, prístup k nej je možný cez referenciu ako k objektu na ploche. Špeciálny význam má preddefinovaná premenná Here, ktorá obsahuje súradnice posledného vykresleného bodu.

x = 1; y = 3;        # numerické premenné
P1: (x,y)            # referencia na bod
p1 = (x,y)           # chyba
u = P1.x; v = P1.y   # zložky suradnice

Poznámka

Je možné používať súradnice zapísané aj bez zátvoriek v tvare x, y, ale z dôvodu možných konfliktov pri expanzii makier je vhodnejší prehľadnejší zápis so zátvorkami (x, y).

line to 1,1
line to (1,1);

Operácie #

Binárne a unárne aritmetické operácie sú definované pre numerické hodnoty, operácie nad súradnicami, ak je to možné, sa konvertujú na operácie nad ich zložkami. Logické operácie sú definované len pre numerické hodnoty, nie je napríklad možné porovnávať medzi sebou dva body.

binárne aritmetické oprácie
+   -   *   /   %   ^

unárne aritmetické operácie
+=   -=   *=   /=   %=

logické operácie 
!=   ==   <   >   >=   <=   ||   &&

Operácie súčtu a rozdielu nad súradnicami sa vyhodnocujú po zložkách pred ich použitím. Násobenie súradnice je možné len numerickou hodnotou a len ako pos-multiplikácia. Príklady použitia:

P1: (1,1)            # atributy P1.x, P1.y
P2: (1,2) + (3,4)    # (4, 6)
P3: (1,1) + P1       # (1+P1.x, 1+P1.y)
P4: P1 + P2
P5: P1 * P2          # chyba 

P6: (P1+P2)/2        # geometrický stred medzi bodmi P1 a P2, 
                     # ekvivalent P6: ( (P1.x + P2.x)/2, (P1.y + P2.y)/2 ) 

line from P1 to P2;
line from (P1.x + 2, 0) to (0, P2.y) + (1,0) to (P3,P1);

P7: (P3, P4)         # ekvivalent P7: (P3.x, P4.y), automatické priradenie

P8: P1*k             # post-multiplikacia, k je skalarna hodnota,  (P1.x*k, P1.y*k)
                     # pre-multiplikacia nie je dovolena
P9: k*P1             # chyba

                     # operacie so zlozkami
P10: (0, P2)         # chyba
P11: (0, P2.y)       # ok

P12: (P1 + 4, P2)    # chyba    
P13: (P1.x+4, P2.y)  # ok

P14: Here;                        # odlozenie aktualnej pozicie
px = Here.x; py = Here.y;         # pristup k zlozkam pozicie
line from Here to Here + (10,10); # Here ma novu hodnotu koncoveho bodu ciary

Pri použití relačných operátorov na súradnice bodov treba príslušnú operáciu realizovať po zložkách

P1 > P2              # chyba
P1.x > P2.x          # ok

Pri kreslení zapojení sa stáva, že musíme presne spojiť dva body zapojenia, ktorých absolútnu polohu nepoznáme. Využitím jednoduchých operácií s referenciami na objekty získame spojenie, ktoré sa nepreruší ani pri dodatočnej zmene polohy objektov.

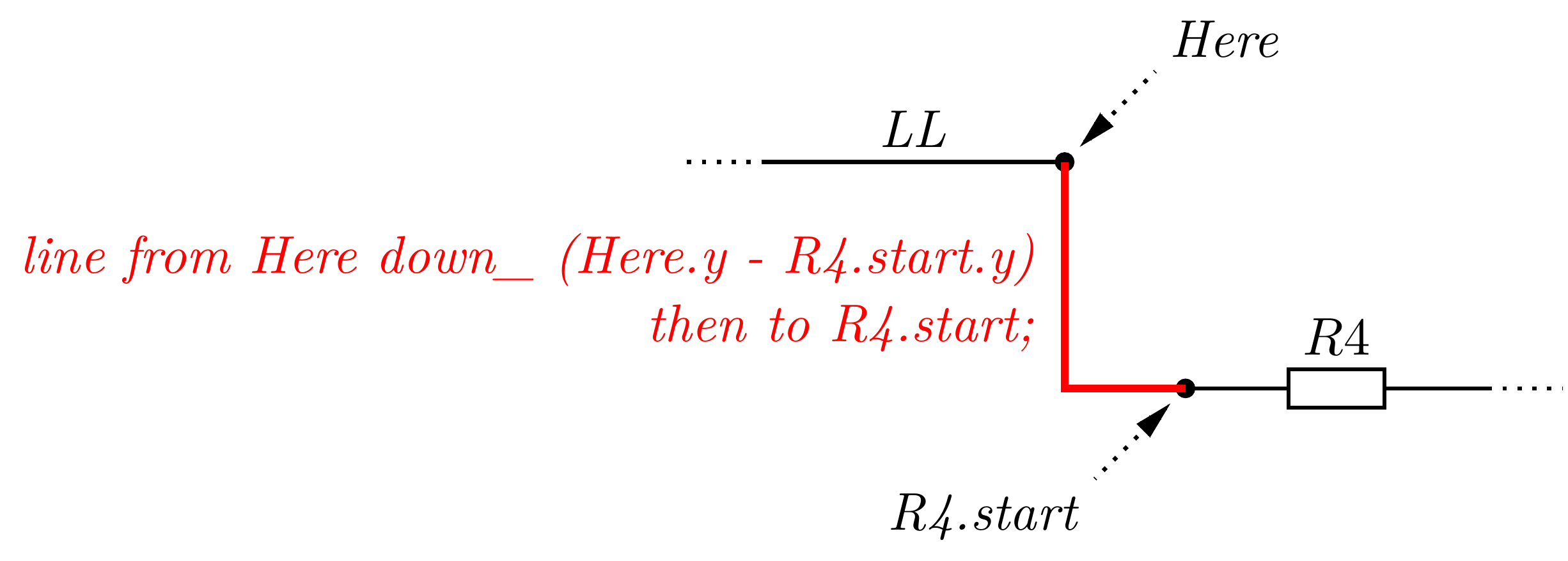
_images/op_001.png

Obr. 39 Použitie numerických operácii pre výpočtu koncového bodu čiary.#

Podobne môžeme využiť výpočet geometrického stredu pre presné umiestnenie textu medzi svorky obvodu.

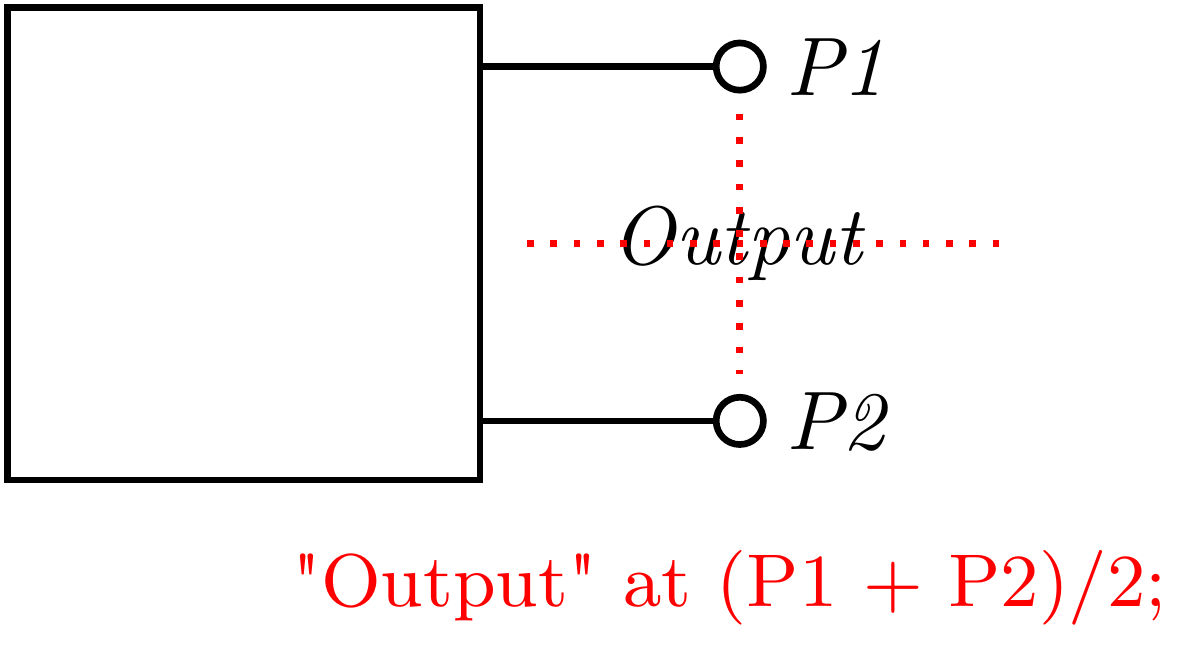
_images/op_002.png

Obr. 40 Text v strede medzi výstupnými svorkami.#

Contents